물리 관련 칼럼을 하나 더 써볼까 하다가,,, 너무 물리만 쓰는 거 같아서 수학도 준비해봤어요!
이 시기에 딱 하기 좋은 수학 공부이기도 하고, 질문을 받아보니 많은 학생들이 도형 공부법에 대해 궁금해하길래
도형 칼럼을 쓰기로 결심했어요
도형 공부가 어려운 이유는 개념과 문제풀이와의 간극이 크기 때문이에요.
개념 자체는 매우 간단한데, 문제풀이에 적용시킬려고 하니 안보이는 경우가 많아요.
여기에는 두 가지 이유가 있어요. 첫 번째 이유로는 기본적인 도형 지식이 없는 경우에요. 중등 기하가 잘 되어있지 않으면 보여야 할 조건들이 보이지 않기 때문이죠. 중등 기하를 아예 모르는 분이면 관련 강의를 수강하는 걸 추천드리고 그래도 적당한 베이스 정도는 있다면 다양한 문제를 풀면서 부족한 개념을 채우시는 걸 추천드립니다.
두 번째 이유로는 연습량 부족이에요! 어떤 조건에 어떻게 대응할지는 연습량이 채워지면서 알 수 있기에 연습량이 부족하다면 도형 문제에서 어려움을 겪으실 수 있어요. 저는 도형 문제를 100~200문제 정도 모아서 한 번에 풀었어요.
도형만 모아놓은 문제집을 들고 그 날 하루 종일 도형만 풀고 푼 김에 그 다음 날도 도형만 풀었던 기억이 나네요. 그렇게 100~200 문제 정도 풀어보니 도형에서 나오는 조건들을 어떻게 문제 풀이에 적용시키는지 종류 별로 보였고, 그 다음부터 도형을 수월하게 풀었던 것 같아요.
하지만 단순히 문제만 많이 푼다고 이러한 어려움이 쉽게 사라지지 않기 때문에, 문제 풀 때 어떤 태도를 갖추어야하는지 설명드리겠습니다!
# 공식을 대하는 태도
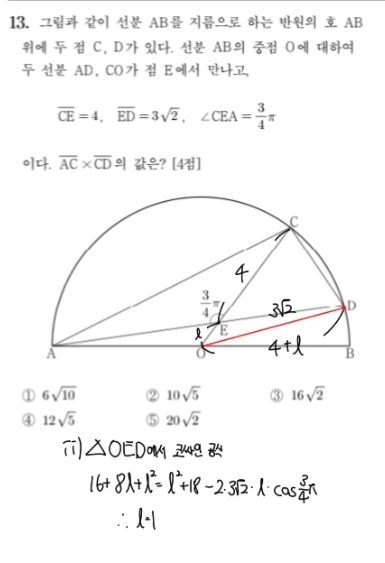
개념만을 배울 때는, 공식을 어떻게 활용할지는 모르고 단순히 공식만을 알고있어요. 이러다보니 문제풀이에 적용이 어려운 것이죠. 그래서 우리가 가져야할 첫 번째 기본 태도는 공식을 '언제' 사용해야하는지를 파악하는 태도를 가져야합니다. 첫 번째로 코사인 공식입니다. 코사인 공식에 활용되는 것들은 세 변과 하나의 각입니다. 따라서 우리는 이 네 가지 중 세 가지를 알고 있는 상황에서 공식을 활용한다는 태도를 가지고 있어야 합니다.
두 번째로는 사인 공식입니다. 사인 공식은 하나의 각, 하나의 변, 반지름 총 세 개를 활용하는 공식이기에 이것들 중 두 개를 알고 하나를 모르는 상황에서 사용하면 되겠죠? 물론 이것은 가장 기본적인 태도들이고, 많은 문제를 푸시면서 유연한 태도들을 챙겨나가시면 됩니다. 삼각형 하나에서 싸인 값의 비율을 알려주면 변 들의 비율로 바로 해석할 수 있는 것처럼 말이죠!
# 문제 과정을 스케치하는 태도
두 번째 태도는 알고 있는 것을 머리 속에 생각하는 태도입니다. 단순히 변의 길이를 구할 수 있는 상황에서 바로 계산해서 구하는게 아닌, 내가 이 변을 알고 있으니 그 다음 문제풀이 과정을 어떻게 전개할지를 생각하면서 푸는 것을 말합니다. 말로만 하면 무슨 뜻인지 잘 모를 수 있기에, 예시와 함께 설명드려보겠습니다.
현재 ABC 삼각형에서 두 변과 하나의 각을 알고 있기에, 우리는 공식을 쓰면 AC를 바로 구할 수 있는 것을 압니다. 그러나 바로 공식을 적용해서 길이를 구하는 것이 아닌, AC를 구한 뒤의 상황을 먼저 생각하는 것입니다. M을 기준으로 할선 정리를 쓰기 딱 좋은 상황인데, M이 중점이니 AM과 MC의 길이도 바로 구할 수 있을 것이고, BM의 길이도 ABM삼각형에서 두 변과 한 각을 아는 상황이기에 바로 구할 수 있으므로 할선 정리로 문제풀이를 마무리 한다는 생각을 한 뒤 길이를 구하시면 문제를 깔끔하게 풀 수 있겠죠?
문제 상황이 조금 더 복잡한 경우에는 이러한 과정을 나눠서 진행하시면 됩니다.
# 가장 중요한 태도
도형 문제 풀 때 제일 열 받는 점은 보조선이라고 할 수 있을 거 같아요. 나는 상상치도 못했는데 갑자기 보조선 딱 긋고 이렇게 푸시면 됩니다~ 이러한 풀이가 많죠. 이러면 나는 도대체 어떻게 공부를 해야하는가에 대한 생각이 들기도 합니다. 비단 보조선 뿐만 아니라 도형 문제 풀이를 보시면 이러한 생각이 들 때도 많죠. 이 때 우리는 낙담만 하면 안됩니다. 이 보조선이 왜 그어져야만 했는지, 왜 이렇게 풀었어야하는지에 대한 당위성을 부여하면서 공부하시다 보면 조금 더 괜찮아 지실겁니다.
이 문제에서 보조선을 왜 그어야할까요? 바로 원에서는 "반지름"이 가장 핵심적인 조건이기 때문입니다. 반지름에서 파생되는 조건(문제풀이에 필요한 요건들)이 가장 많기 때문에, 우리는 원이 나온다면 반지름에 항상 집중해야합니다. 이러한 당위성을 부여하신다면, 다음에 원 관련 문제에 나왔을 때 조금 더 쉽게 대처할 수 있겠죠?
이 부분이 도형 공부법에서 가장 중요한 부분이에요! 내가하는 행동들에 당위성을 부여하다보면 어떤 조건이 나왔을 때 어떻게 반응해야하는지 바로바로 생각이 나기 때문에 이 부분에 집중해서 도형 공부를 하시면 좋은 성적을 거둘 수 있을 것이라고 생각해요.
그 뒤 풀이로는 코싸인 공식 두 번 활용 / 사인 공식 활용 / 할선 정리가 있겠네요!
이렇게 문제 상황을 보고 어떻게 조건을 활용해야하는지는 다음 칼럼에서 정리해드리겠습니다
정리한 것을 바탕으로 나는 어떤 조건을 먼저 볼건지 간략하게 순서를 결정해놓으시는 것도 많은 도움이 될 거에요!
( 다음 칼럼 내용 )
3. 문제 유형 정리
그러면 이제 문제를 풀면서 어떤 연습을 해야할까요? 도형 문제들은 대체적으로 나온 유형이 상황만 달라져서 많이 나옵니다. 따라서 첫 번째로는 이 조건에서는 어떻게 반응해야할지를 연습하고 두 번째로는 무엇을 먼저 볼 것인지 정하는 것입니다. 먼저 볼지에 대한 순서는 완벽하게 정할 필요는 없습니다. 문제 상황마다 먼저 봐야하는 것들이 달라지는 경우가 많기에 대략적으로 어떤 것들을 먼저 보겠다는 정도만 정하시면 됩니다. 저 같은 경우 원이 나오면 반지름 활용, 원주각, 원주각에서 파생되는 같은 변 정도를 먼저 보겠다는 정도만 챙기고 갔습니다.
1. 사인공식->길이변으로해석
2. 보각 합이 180도
3. 접현각
4. 같은 현 활용
5. 이등변
6. 넓이 두 가지 해석
7. 원주각, 중심각
8. 각변환
9. 닮음










 원광대학교 한의예과
원광대학교 한의예과